Arman Maesumi

arman_maesumi@brown.edu

I am a final year computer science PhD student at Brown University, where I am advised by Professor Daniel Ritchie. My work is supported by the NSF Graduate Research Fellowship Program.

I received my BS in computer science from The University of Texas at Austin in 2021, where I did research with Professor Chandrajit Bajaj.

My research interests lie at the intersection of deep learning and computer graphics. In my free time I enjoy creating 3D art, cooking, and playing chess.

I am actively looking for full-time opportunities starting in 2026!

Geometry ↔ Learning: My research considers the interplay of geometry and deep learning as a two-way street.

1) Deep learning for geometry:

I am actively developing robust and efficient neural methods for large-scale, in-the-wild 3D data, with the goal of extending the deep learning revolution to the 3D world.

Viewing feature spaces through a geometric lens has enabled emergent capabilities in my research; e.g., by enabling generative models to smoothly interpolate data in the absence of in-between observations.

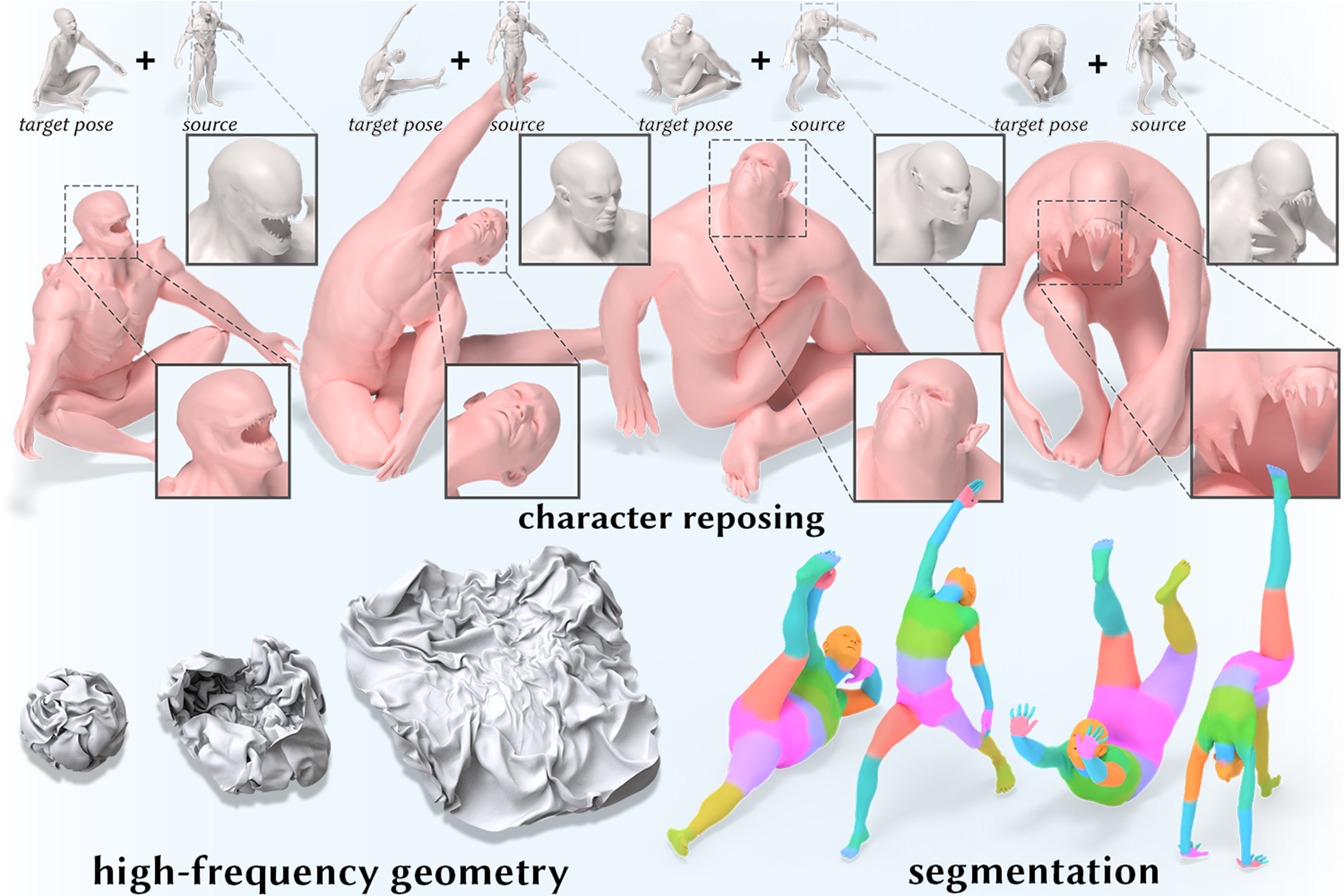
Arman Maesumi, Tanish Makadia, Thibault Groueix, Vladimir G. Kim, Daniel Ritchie, Noam Aigerman
ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia), 2025
[ project page / pdf (64mb) / code / bibtex ]

A new neural architecture for learning on surfaces that overcomes several key deficiencies in existing methods. We demonstrate its ability to learn deformations of detailed, high-resolution meshes, as well as semantic segmentation.

Arman Maesumi, Dylan Hu, Krishi Saripalli, Vladimir G. Kim, Matthew Fisher, Sören Pirk, Daniel Ritchie
ACM Transactions on Graphics (Proceedings of SIGGRAPH), 2024
[ project page / pdf (34mb) / arXiv / code / bibtex ]

A data augmentation strategy that enables diffusion models to smoothly interpolate between disjoint data modes. We train a diffusion model to blend multiple types of procedural noise patterns, even in the absence of "in-between" training data.

Arman Maesumi, Paul Guerrero, Vladimir G. Kim, Matthew Fisher, Siddhartha Chaudhuri, Noam Aigerman, Daniel Ritchie
SIGGRAPH Asia, 2023 (Conference Track)
[ project page / pdf (30mb) / arXiv / bibtex ]

What is the smoothest subspace that spans a set of points in latent space? We optimize smooth parametrizations of such subspaces in 3D generative models and use them to explore continuous variations of meshes.

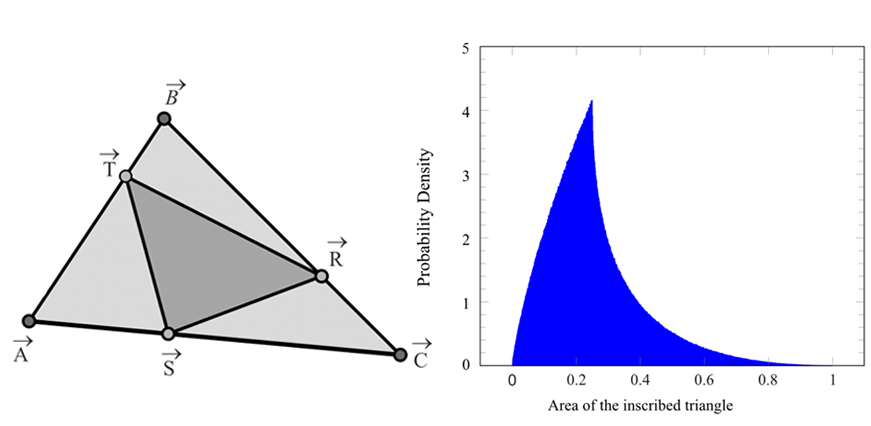
The probability density function and moments (OEIS A279055) of the area of stochastically generated inscribed geometry are derived.

Preliminary findings were presented at TUMC 2017.

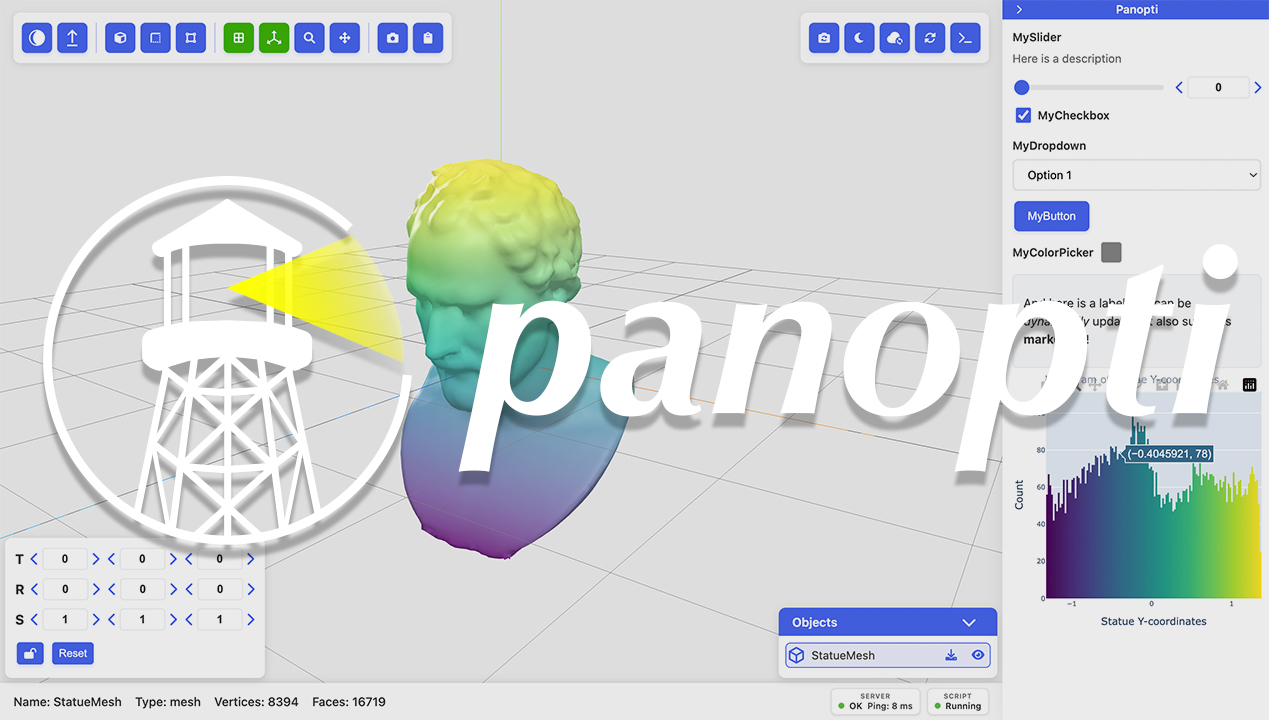
A Python package for interactive 3D visualization that seamlessly supports remote development setups (e.g. through SSH) and headless rendering.

CUDA kernels that accelerate construction of discrete differential operators on meshes, very useful e.g. when used in a training loop for geometric problems.

A PyTorch-based RBF Interpolator that supports auto-diff and is much faster than SciPy's CPU implementation.

In my free time, I enjoy creating 3D renderings and physical simulations using various software. More can be found here. The programs and tools that I use include: Blender, Cinema 4D, RealFlow, Vray, Octane, Arnold, Krakatoa, and more.

Template