|
|
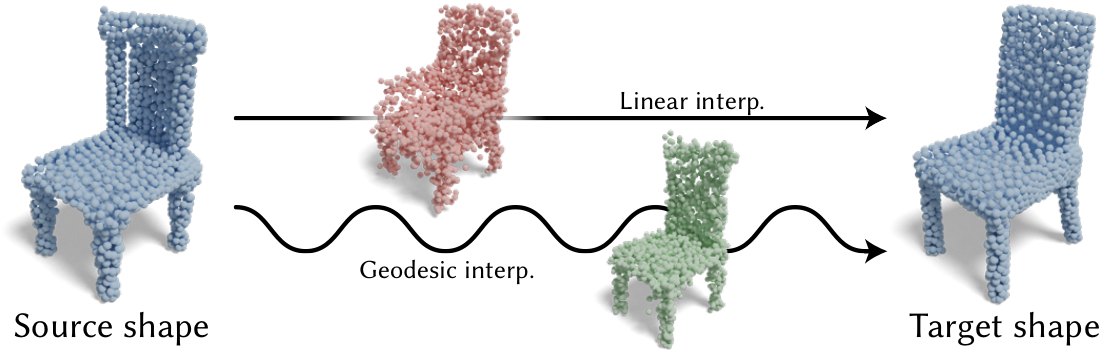
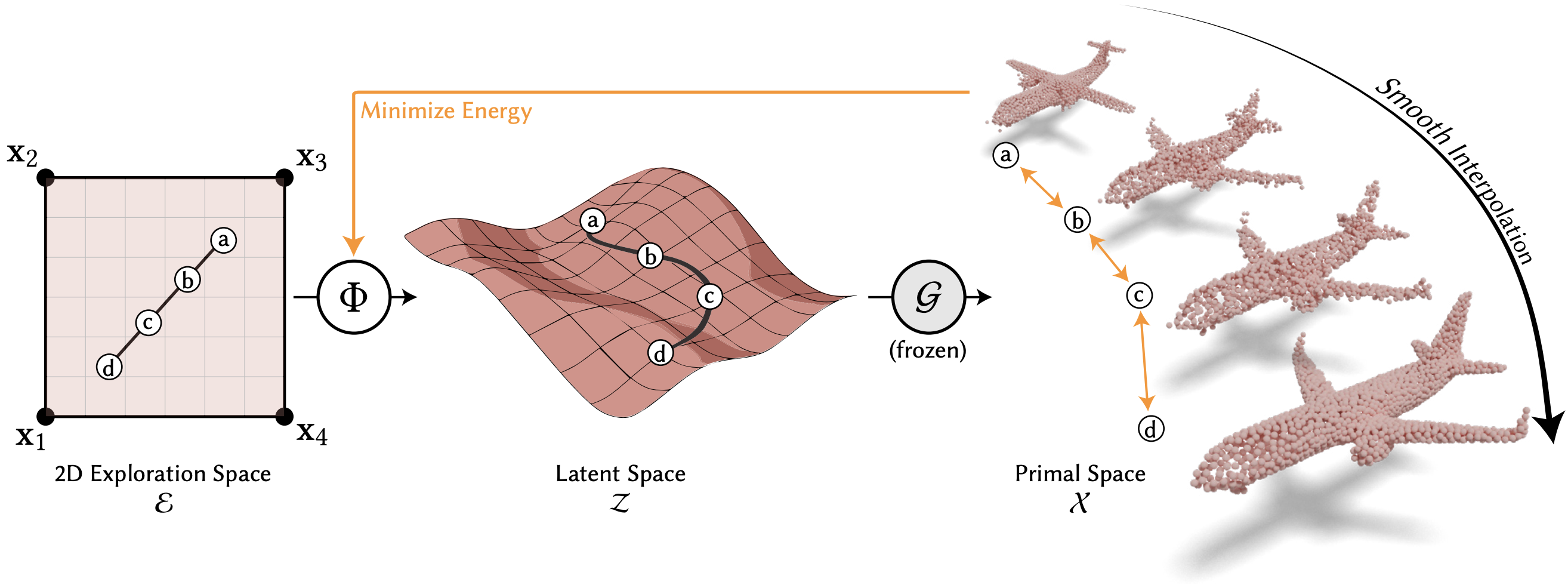
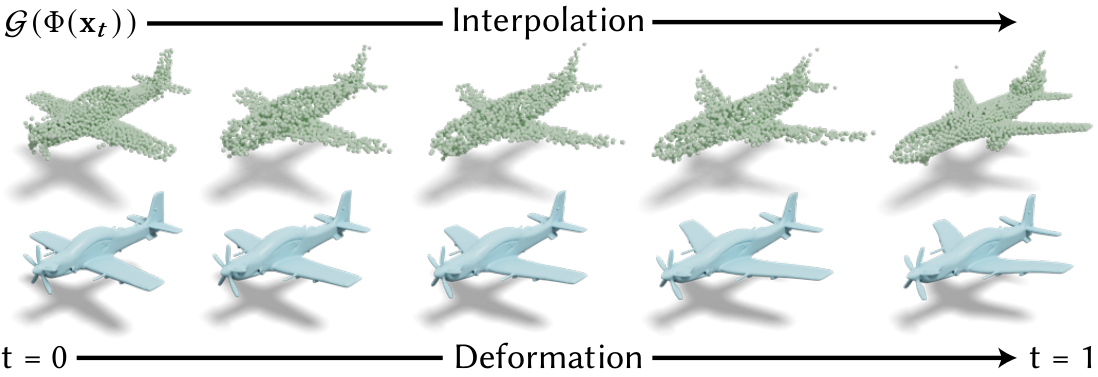
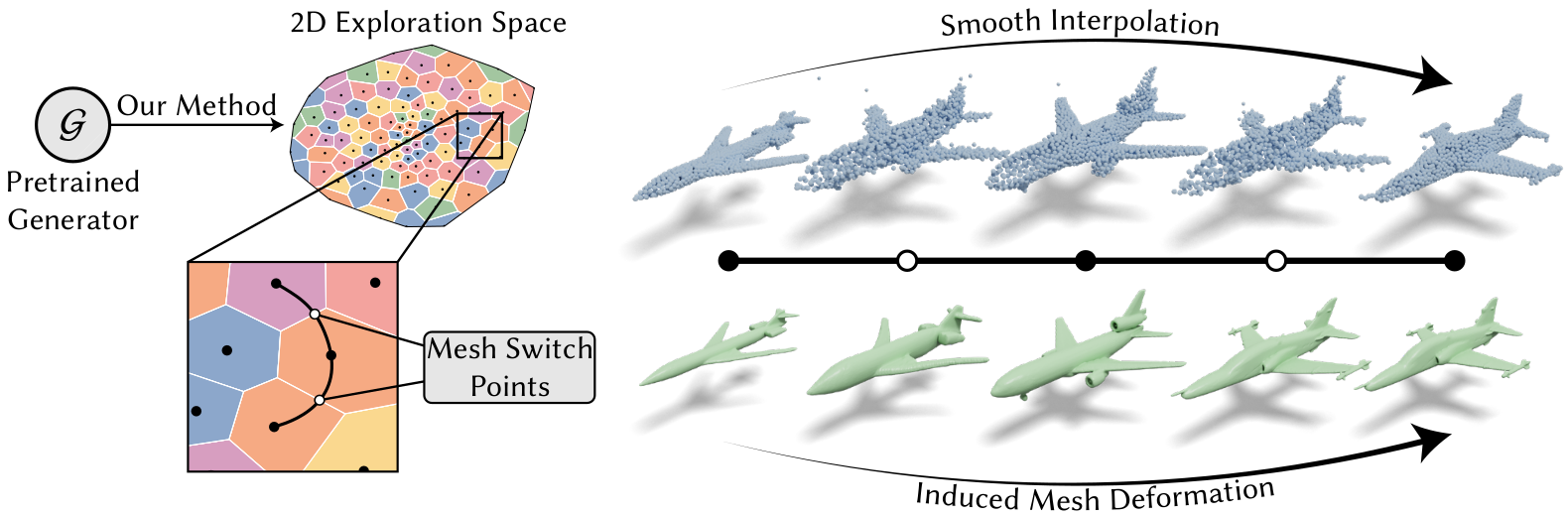
Figure 1. We present a method to explore variations among a given set of input shapes (denoted by black Voronoi centers on the left) using a two-dimensional exploration space. This exploration space smoothly and naturally interpolates between the input shapes by constructing a mapping to a sub-space of a pre-trained generator's latent space that optimizes the smoothness of interpolations along any trajectory. Additionally, we transfer the variation over these interpolation trajectories onto the original high-quality meshes, avoiding loss of detail from the unstructured generator output. |