Procedural noise is a fundamental component of computer graphics pipelines, offering a flexible way to generate textures that exhibit "natural" random variation. Many different types of noise exist, each produced by a separate algorithm. In this paper, we present a single generative model which can learn to generate multiple types of noise as well as blend between them. In addition, it is capable of producing spatially-varying noise blends despite not having access to such data for training. These features are enabled by training a denoising diffusion model using a novel combination of data augmentation and network conditioning techniques. Like procedural noise generators, the model's behavior is controllable via interpretable parameters plus a source of randomness. We use our model to produce a variety of visually compelling noise textures. We also present an application of our model to improving inverse procedural material design; using our model in place of fixed-type noise nodes in a procedural material graph results in higher-fidelity material reconstructions without needing to know the type of noise in advance.

Goal: Learn a denoising diffusion model that can produce multiple types of parametrized noise functions and blend between them spatially.

Problem: Training a denoising U-Net without spatially-varying noise data results in poor adherence to the conditioning signal.

Insights:

1. The U-Net's bottleneck architecture causes a smearing effect on the network's learned features.


2. Spatially-varying synthesis requires the U-Net to denoise along multiple denoising trajectories simultaneously, which is difficult in the absence of spatially-varying noise data.

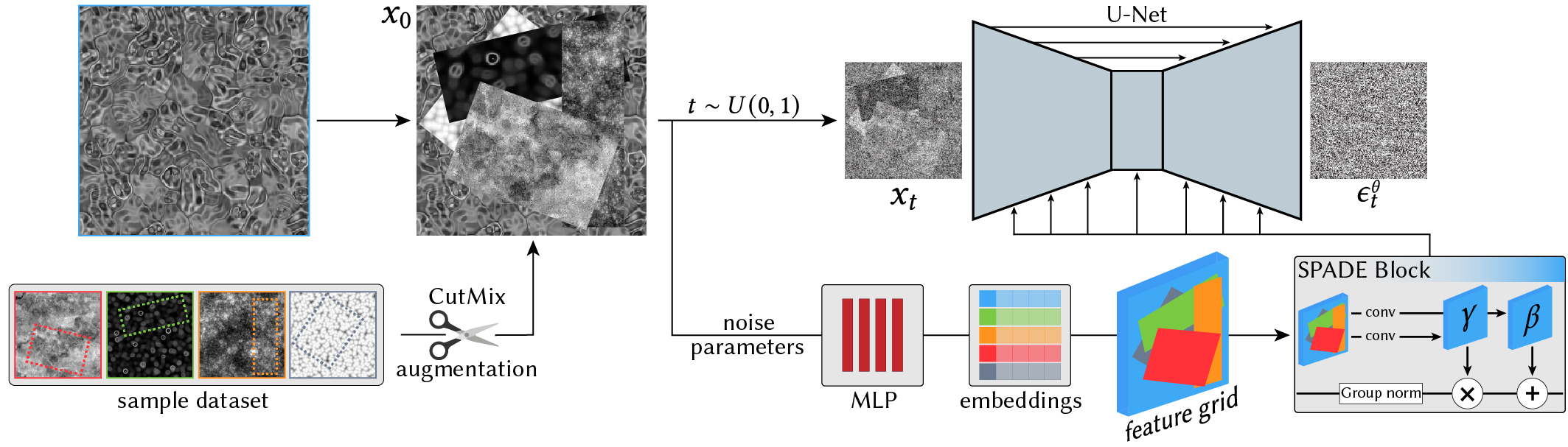
Figure 3. During training, we first transform the current data sample (highlighted in blue) by cutting and patching together a set of other random samples from the dataset, resulting in a training image x₀. The noise parameters for each image patch are passed to an MLP, which projects the parameter sets into an embedding space that encodes both the noise type (class) and the noise parameters. The resulting feature vectors are tiled to form a feature grid, which is used as a conditioning signal in the U-Net's SPADE blocks.

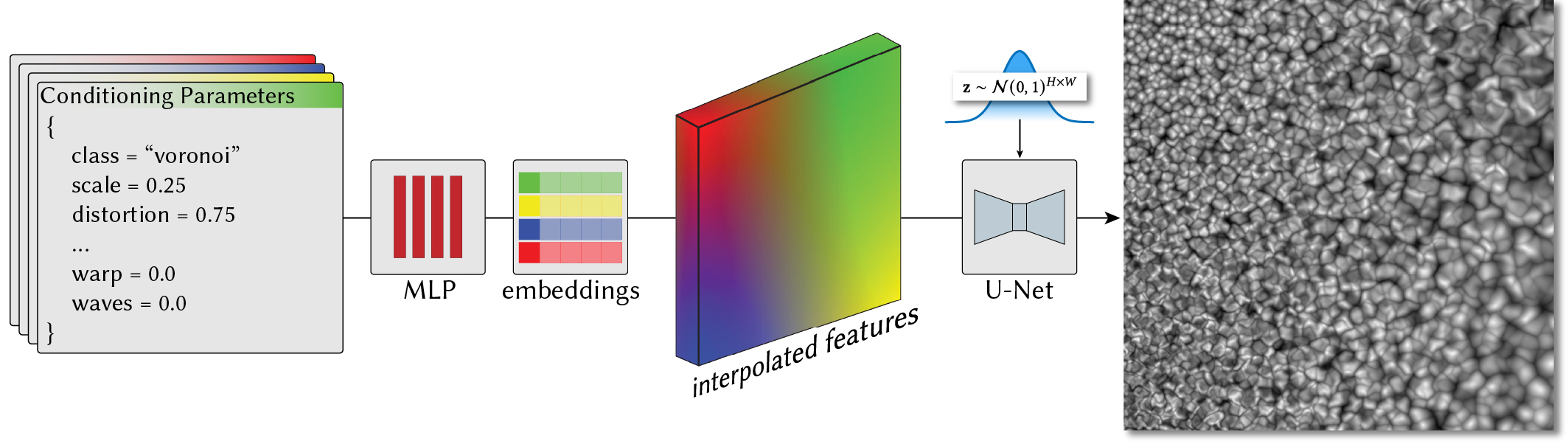
Figure 4. At inference time, we query our network using artificially constructed feature grids, enabling a flexible way to synthesize spatially-varying noise patterns. Here we embed four sets of noise parameters, pictorially shown as one of four colors. We blend the feature vectors using bilinear interpolation, creating a smoothly-varying feature grid, which our U-Net is able to transform into a Voronoi noise pattern with non-uniform scale and distortion characteristics.

We demonstrate that our model can be used as a differentiable proxy for noise generator nodes in a procedural material graph. Using our model in place of fixed-type noise nodes results in higher-fidelity material reconstructions.

Figure 7. Given a procedural material graph and a target photograph, our noise generative model serves as a useful prior over the space of noise functions, facilitating the recovery of non-trivial patterns that are present in the target photos, and improving the baseline result given by MATch. Two similarity scores are reported for each result with respect to the target image: MATch's feature-based texture similarity metric (left) and LPIPS (right). Lower is better for both scores.

Figure 10. After optimization, we can easily modify the resulting procedural material graphs. Here a marble material graph is optimized (first row), and edited in various ways (second row). We show the results of editing the noise colorization, resampling our diffusion noise, and modifying our model's conditioning inputs.